Emily takes a very intuitive approach to understanding the relative sizes of her lists (even, threeven, fiven, seven’n etc.) and the segments they create. However, we really should look a little deeper into the mathematics.
Emily’s assertion that the lists of even and odd numbers are the same size is correct – because they are both infinite. Interestingly, when we combine the even and odd numbers we have all the positive integers which are also infinite.
When Emily creates the threeven list, she uses a third of the odd numbers. Her intuition is that, with just the even and threeven numbers separated, the lists have the following relative sizes:
- 1/2 even
- 1/6 threeven
- 1/3 oddish
However, we have seen that when we add two infinite lists the resulting list is also infinite. In the same way, when we take a third of an infinite list the result is still infinite.
A better way to think about the relationships between the lists is with probabilities. If we choose positive integers at random, half the time they will be odd and half the time they will be even.
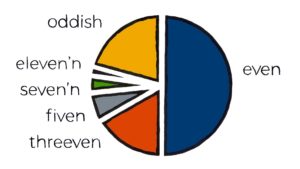
A third of the time a random positive integer will be threeven. A fiven number will occur, on average, twice in every thirty selections. And so on, with the fractions Emily calculated.

Recent Comments