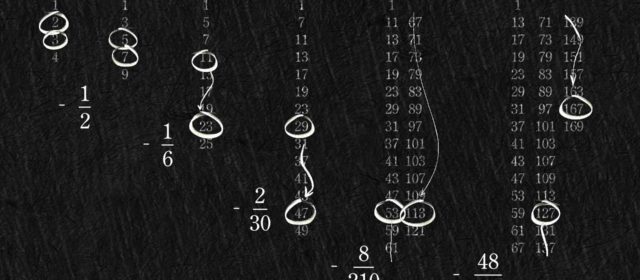
The primorial numbers emerge from the fractions that Emily calculates. The primorials form an integer sequence which is created by multiplying successive prime numbers. The first in the sequence is the first prime number: The second in the sequence is: The third is: Then: And so on. The numbers get quite big, very quickly. The term...
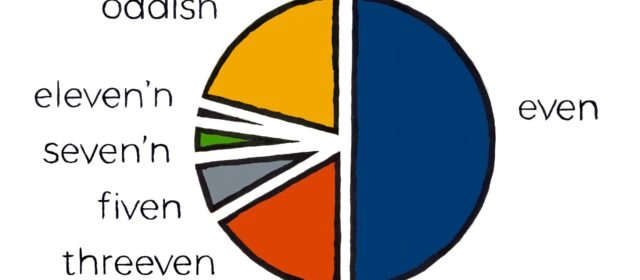
Read MoreEmily invents the threeven numbers as the subset of the odd numbers that all have three as a factor. She knows, intuitively by looking at her counting numbers, that a third of all positive integers are divisible by three with no remainder. She can also see in her numbers that half of these numbers have already been counted in the even numbers. So, to calculate the portion of threeven numbers: And the portion of remaining...
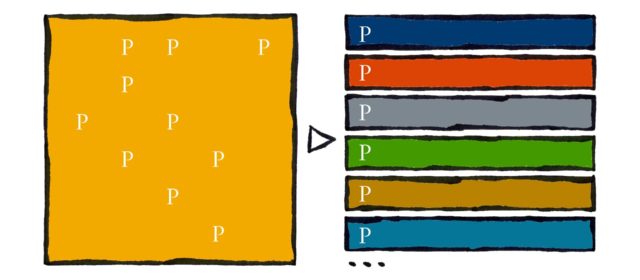
Read MoreThis is the table of 144 numbers that Emily, and millions like her, are drilled on every week at school. The numbers have been colour-coded to their lowest prime factor according to Emily’s scheme. Each number is repeated 2.5 times on average and some numbers appear 6 times. The table only contains the safe, friendly and boring numbers. Here is another table of 144 numbers with each appearing only once. We can see the odd...
Read MoreEmily takes a very intuitive approach to understanding the relative sizes of her lists (even, threeven, fiven, seven’n etc.) and the segments they create. However, we really should look a little deeper into the mathematics. Emily’s assertion that the lists of even and odd numbers are the same size is correct – because they are both infinite. Interestingly, when we combine the even and odd numbers we have all the...
Read MoreWhen Emily makes the decision to exclude the even numbers from her threeven list she establishes her method to ensure that all her lists have unique elements. If we consider each list (even, threeven, fiven, seven’n etc.) to be a set then we can say that they are all disjoint. She starts with a single, infinite set of positive integers with the prime numbers scattered throughout. By applying her...
Read MoreThe sequences of integers that Emily finds in her exploration of numbers are well known to mathematicians. The On-Line Encyclopedia of Integer Sequences (OEIS) was started by Neil J. A. Sloane in 1964 and is a valuable open resource. Here are the lists of numbers that Emily created and their reference numbers: A000027 Everyday counting numbers (positive integers) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,...
Read More



Recent Comments